Fahrzeugleistung anpassen: Unterschied zwischen den Versionen
(→Theorie: Unterschied zwischen Bremskraft und Antriebskraft) |
(→Theorie: Unterschied zwischen Bremskraft und Antriebskraft) |
||
| Zeile 37: | Zeile 37: | ||
Einfach gesagt kann man mit Antriebskraft schneller werden, mit Bremskraft niemals - das wär ja dann sonst sehr energieeffizient! ;) | Einfach gesagt kann man mit Antriebskraft schneller werden, mit Bremskraft niemals - das wär ja dann sonst sehr energieeffizient! ;) | ||
| − | Es ist ziemlich schwierig und aufwändig, wenn man Bremskräfte korrekt simulieren will - und zwar genau in dem Moment, wo das Auto stehen bleibt: Während man noch fährt, wirkt sie einfach der Bewegung entgegen. Fahr ich vorwärts, treibt der Motor ebenfalls vorwärts, wenn ich dann bremse, wirkt die Bremskraft rückwärts. In dem Augenblick aber, wo das Auto stehen bleibt, verschwindet die Bremskraft schlagartig (weshalb man nämlich auch beim Anhalten hinfallen kann, wenn der Busfahrer nicht die Bremskraft vor Stillstand reduziert). Im Stand nun "versucht" die Bremskraft, alle restlichen auftretenden Kräfte auf Null zu kompensieren, z.B. Hangabtrieb in einem Gefälle oder schlicht die Antriebskraft, sofern man im Stand bei angezogener Handbremse losfahren möchte. Wenn diese anderen Kräfte zu groß werden und die maximale Bremskraft (die nämlich, die über das Script vorgegeben wird) überschreiten, dann kann die Bremse das Fahrzeug nicht mehr halten und es roll los. Nun gilt aber wieder "andere" Variante: Die Bremskraft wirkt nun wieder "gegen" die Geschwindigkeit. | + | Es ist ziemlich schwierig und aufwändig, wenn man Bremskräfte korrekt simulieren will - und zwar genau in dem Moment, wo das Auto stehen bleibt: Während man noch fährt, wirkt sie einfach der Bewegung entgegen. Fahr ich vorwärts, treibt der Motor ebenfalls vorwärts, wenn ich dann bremse, wirkt die Bremskraft rückwärts. In dem Augenblick aber, wo das Auto stehen bleibt, verschwindet die Bremskraft schlagartig (weshalb man nämlich auch beim Anhalten hinfallen kann, wenn der Busfahrer nicht die Bremskraft vor Stillstand reduziert). Im Stand nun "versucht" die Bremskraft, alle restlichen auftretenden Kräfte auf Null zu kompensieren, z.B. Hangabtrieb in einem Gefälle oder schlicht die Antriebskraft, sofern man im Stand bei angezogener Handbremse losfahren möchte - sie kann aber niemals ''mehr'' bewirken, als diese Kräfte zu kompensieren. Wenn diese anderen Kräfte zu groß werden und die maximale Bremskraft (die nämlich, die über das Script vorgegeben wird) überschreiten, dann kann die Bremse das Fahrzeug nicht mehr halten und es roll los. Nun gilt aber wieder "andere" Variante: Die Bremskraft wirkt nun wieder "gegen" die Geschwindigkeit. |
Dies alles betrifft die Antriebskraft aber nicht: Sie wirkt immer 100% in die vorgegebene Richtung, egal ob und in welche Richtung das Fahrzeug rollt! | Dies alles betrifft die Antriebskraft aber nicht: Sie wirkt immer 100% in die vorgegebene Richtung, egal ob und in welche Richtung das Fahrzeug rollt! | ||
| + | |||
| + | Energetisch gesprochen: Während die Antriebskraft beliebig wirken können darf, kann die Bremskraft nur so wirken, dass sie dem Fahrzeug kinetische Energie entzieht (Bremsen werden warm), aber ihm niemals Energie zuführt. | ||
Aus diesem Grund gibt es die besagte Unterteilung: | Aus diesem Grund gibt es die besagte Unterteilung: | ||
Version vom 30. August 2012, 21:07 Uhr
Hinweis: Dieser Artikel wurde noch nicht ins Englische übersetzt!
In diesem Artikel wird beschrieben, wie in OMSI die Fahrzeugleistung berechnet wird und wie man diese anpassen kann.
Inhaltsverzeichnis
Theorie: Kraft und Drehmoment
Der Begriff Kraft ist aus dem Alltag bekannt: Möchte man ein Kilogramm gegen die Schwerkraft anheben, so benötigt man 9,8 - also ungefähr 10 - Newton (N) Kraft. Man könnte also sagen: Eine Kraft von 10 Newton "fühlt sich so an" wie 1 kg. Physikalisch natürlich sinnlos, aber so kann man es sich grob vorstellen! ;)
Mit derselben Kraft kann man aber auch einen Gegenstand von 1 kg (reibungsfrei und ohne rotierende Elemente) um 35 km/h innerhalb einer Sekunde beschleunigen. Wenn ihr also das nächste Mal beim Eislaufen eine Milchpackung (1 Liter Milch ist etwa 1 kg schwer) dabei habt, könnt ihr das testen...! :D Denn 9,8 Newton (also "gefühlt" 1 kg) Kraft erlaubt eine Beschleunigung von 9,81 Meter pro Kilogramm und Quadratsekunde. Quadratsekunde? OK, klingt merkwürdig... Sagen wir besser: 9,81 Meter/Sekunde pro Kilogramm und pro Sekunde. 9,81 m/s sind aber gerade 35 km/h, es heißt also nichts anderes, als ich oben bereits gesagt hab! :)
Soweit, so verständlich - hoffentlich...
Kommen wir nun zu etwas, was theoretisch bei weitem nicht jedem bekannt ist: Dem Drehmoment! (Ja, es heißt das Moment, wenn hiervon die Rede ist.)
Die oberen Beispiele bezogen sich nämlich auf lineare Bewegungen. Diese misst man in Metern, deren Geschwindigkeit in Meter/Sekunde (oder km/h) und deren Kräfte in Newton.
Wenn man nun aber versucht, ein Marmeladenglas aufzumachen - was passiert hier? Die "Strecke", die man zurücklegt, misst man doch in Grad? (Oder physikalisch besser: im Bogenmaß / Rad). Der Deckel bewegt sich ja nicht vom Fleck weg - er verdreht sich nur, und trotzdem kostet es Kraft - aber diese kann man nicht in Newton ausdrücken.
Aus diesem Grund wurde das Moment / Drehmoment eingeführt: Es hat die Einheit Newtonmeter, also Newton mal Meter.
Ein ausgesprochener Schwächling schafft es mal gerade so, eine Tafel Schokolade anzuheben (100g = 1 Newton). Er bekommt das Marmeladenglas nur gerade so mit einem Hebel auf, der einen Meter lang ist! Dann hat er einen Newton mit einem Hebelarm von einem Meter angewendet, sodass im Drehpunkt letztlich ein ein Newtonmeter gewirkt hat.
Sein Kumpel ist stärker: Er bekommt das Glas mit einem nur 10cm langen Hebel auf. Dieser ist demnach nur ein Zehntel so lang (0,1 m) - also benötigt er die zehnfache Kraft (10 N), sodass am Ende wieder genau 1 Nm herauskommt.
Und am Autorad ist es genauso: Motor, Getriebe und Differenzial übertragen ihre Kräfte mit Hilfe von Wellen, also drehenden Objekten, sodass man die Stärke dieser Kraft demzufolge auch in Nm angeben muss - und auch hier vom Drehmoment spricht.
Wer es jetzt nicht verstanden hat, möge sich bitte im Internet weiterbilden (www.wikipedia.de).
Theorie: Unterschied zwischen Bremskraft und Antriebskraft
Warum gibt es zwei getrennte Variablen für Antriebskraft/-moment und Bremskraft? Ist die Bremskraft nicht einfach negativ?
Neeeeee, so einfach ist es leider nicht! :) Was ist denn, wenn man rückwärts fährt?
Das Problem ist folgendes:
Einfach gesagt kann man mit Antriebskraft schneller werden, mit Bremskraft niemals - das wär ja dann sonst sehr energieeffizient! ;)
Es ist ziemlich schwierig und aufwändig, wenn man Bremskräfte korrekt simulieren will - und zwar genau in dem Moment, wo das Auto stehen bleibt: Während man noch fährt, wirkt sie einfach der Bewegung entgegen. Fahr ich vorwärts, treibt der Motor ebenfalls vorwärts, wenn ich dann bremse, wirkt die Bremskraft rückwärts. In dem Augenblick aber, wo das Auto stehen bleibt, verschwindet die Bremskraft schlagartig (weshalb man nämlich auch beim Anhalten hinfallen kann, wenn der Busfahrer nicht die Bremskraft vor Stillstand reduziert). Im Stand nun "versucht" die Bremskraft, alle restlichen auftretenden Kräfte auf Null zu kompensieren, z.B. Hangabtrieb in einem Gefälle oder schlicht die Antriebskraft, sofern man im Stand bei angezogener Handbremse losfahren möchte - sie kann aber niemals mehr bewirken, als diese Kräfte zu kompensieren. Wenn diese anderen Kräfte zu groß werden und die maximale Bremskraft (die nämlich, die über das Script vorgegeben wird) überschreiten, dann kann die Bremse das Fahrzeug nicht mehr halten und es roll los. Nun gilt aber wieder "andere" Variante: Die Bremskraft wirkt nun wieder "gegen" die Geschwindigkeit.
Dies alles betrifft die Antriebskraft aber nicht: Sie wirkt immer 100% in die vorgegebene Richtung, egal ob und in welche Richtung das Fahrzeug rollt!
Energetisch gesprochen: Während die Antriebskraft beliebig wirken können darf, kann die Bremskraft nur so wirken, dass sie dem Fahrzeug kinetische Energie entzieht (Bremsen werden warm), aber ihm niemals Energie zuführt.
Aus diesem Grund gibt es die besagte Unterteilung:
Bremskräfte:
- Radbremsen
- Luftwiderstand
- reibende Bremsen im Antriebsstrang
Antriebskräfte:
- Motor
- Retarder
- hydraulische oder elektrische Bremsen
Überblick OMSI.exe <=> Script
Zunächst ist zu unterscheiden, welcher Teil der Fahrzeugphysik in der OMSI.exe berechnet wird und welcher Teil im Script berechnet wird - denn: Alle physikalischen Eigenschaften, die OMSI.exe zur Physikberechnung verwendet werden, werden über die *.ovh- oder *.bus-Datei justiert, wohingegen alle Eigenschaften, welche im Script zur Anwendung kommen, in den dortigen Konstanten-Dateien eingetragen sind.
Die OMSI.exe berechnet
- die Interaktion Reifen <=> Straße
- die Bewegung des Fahrzeuges infolge dieser Interaktion
- Kollisionen
- die KI, sofern das Fahrzeug ein KI-Fahrzeug ist
- Interaktion mit anderen KI-Fahrzeuge und Fußgängern sowie Fahrgästen am oder im Bus
Das Script berechnet
- das Drehmoment, welches an den Rädern anliegt, sowie die Bremskraft
- Cockpitanzeigen
- Türen
- Heizung / Klimaanlage
- Sonstige Systeme im Fahrzeug
Da es in diesem Artikel vor allem um die Fahrzeugleistung geht - also letztendlich darum, was für ein Drehmoment am Rad auftritt - haben wir es fast ausschließlich um eine scriptseitige Programmierung zutun.
Das war auch genauso beabsichtigt: Denn bekanntlich gibt es verschiedene Antriebsformen, welche ihrerseits auch in den Details sehr unterschiedlich sein können: Vor allem im Bereich der Automatikgetriebe gibt es herstellerabhängig prinzipielle Unterschiede, welche sich nicht bloß durch Anpassung von Konstanten darstellen lassen, sondern einen anderen Code benötigen.
Rad-Script-Interaktionen
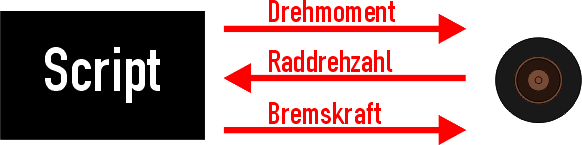
In der nebenstehenden Abbildung ist nun aufgegliedert, welche Interaktionen zwischen physikalisch simuliertem Rad (in der OMSI.exe) und dem Script geschehen:
- Jedes Rad liefert seine Drehzahl (Variablen: n_Wheel als Durchschnittswert oder pro Rad Wheel_RotationSpeed_#_L/R, Einheit: Umdrehungen pro Minute)
- Das Script kann jedem Rad ein gewisses Drehmoment auferlegen (Variable: M_Wheel als Summe auf alle als angetriebene ausgewiesenen Achsen, Einheit: kNm)
- Ferner kann das Script allen Rädern zusammen oder pro Rad eine Bremskraft auferlegen (Variable: Brakeforce als Kraft für alle Räder zusammen oder Axle_Brakeforce_#_L/_R pro Rad, Einheit: N)
Änderung der Fahrzeugleistung des SD202
Da die Fahrzeugleistung also komplett vom Script berechnet wird, ist sie sehr stark vom Fahrzeugscript abhängig. Wir müssen uns also ein Fahrzeug aussuchen, welches wir anpassen wollen - wir nehmen einfach den SD202 D92. Aber letztlich sind die Fahrzeuge, was die Leistungsberechnung angeht, ohnehin gleich.
Übersicht der interessanten Scriptdateien
Wichtig sind zwei Bereiche von Scriptdateien: "Antrieb" für Getriebe und Differenzial, "Engine" für den Motor.
Außerdem beschränken wir uns hier auf die reine Manipulation von Konstanten. Dies heißt leider auch, dass das Einfügen weiterer Gänge ersteinmal außen vor bleiben muss.
Aus diesem Grunde bleiben zwei Dateien übrig, welche die wichtigsten Parameter der Fahrleistung enthalten:
- antrieb_constfile_D88.txt (ist für alle Busse zwischen D88 und D92 zuständig)
- engine_constfile_D92.txt
Schritt A: Die Kraft des Motors
Der Motor ist eine Blackbox, die Benzin in Drehmoment umwandelt. Wie jeder aus Erfahrung weiß, geht das nur bis zu einer gewissen Drehzahl, darüber passiert nix mehr. Außerdem ist das Drehmoment abhängig von der Gaspedalstellung: Je mehr Gas, desto mehr Kraft.
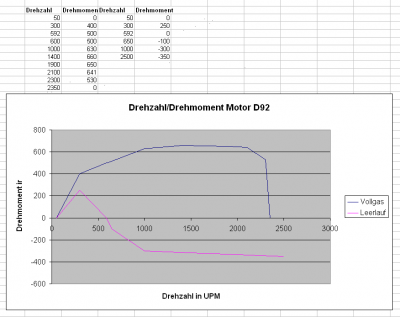
Zuständig hierfür sind in der engine_constfile_D92.txt die Funktionen "engine_M_minThrottle" und "engine_M_maxThrottle": Es handelt sich hierbei um Sammlungen von Wertepaaren Drehzahl/Drehmoment. Diese lassen sich natürlich auch (bspw. in Excel) als Diagramm darstellen:
Damit hätten wir also die erste Möglichkeit, das Fahrzeug zu tunen:
- Erhöhen der maximalen Kraft des Motors für bestimmte Drehzahlbereiche oder komplett
- Veränderung der Leerlaufdrehzahl (wo die magentafarbene Linie die X-Achse erneut schneidet)
- Veränderung der Höchstdrehzahl (wo die blaue Linie die x-Achse erneut schneidet)
- Generelle Änderung des Verlaufes in sonstiger Weise
Man kann also bspw. alle y-Werte verdoppeln - dann erhält man einen doppeltstarken Motor (realistisch) oder man kann alle x-Werte verdoppeln, dann erhöht sich entsprechend die Höchstgeschwindigkeit, dies ist aber ziemlich unrealistisch, weil man sich damit schnell aus dem Bereich realistischer Motorphysik hinausbewegt; außerdem muss ggf. der Motorsound angepasst werden, weil der für hohe Drehzahlen nicht ausgelegt ist.
Am Besten natürlich, man besorgt sich ein reales Drehzahl-Drehmoment-Kennfeld und liest daraus die Werte ab.
Wo steht denn jetzt aber die Motorleistung in PS???
Die Motorleistung ist nur implizit enthalten! Physikalisch berechnet sich die Motorleistung als Drehzahl mal Drehmoment, wird also ebenfalls über den Drehmomentverlauf beeinflusst. Um nun den Motor mit einer bestimmten Höchstleistung zu versehen, müssen wir nochmal die Excel-Tabelle bemühen - wir fügen hierzu noch je eine Leistungstabelle ein, welche die folgende Formel enthält: =B4*2*PI()/60*C4/1000
Hierbei wird zunächst die Drehzahl (B4) von UPM in Rad/s umgerechnet, dann wird mit dem Moment (C4) multipliziert und schließlich (zur Umrechnung von Watt in Kilowatt) durch 1000 geteilt.
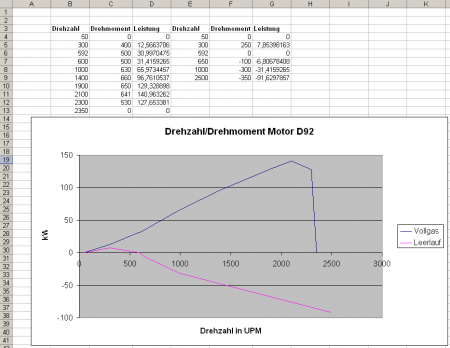
Ergebnis ist das Drehzahl-Leistungs-Diagramm:
Offensichtlich ist hier also eine Höchstleistung von knapp 150 kW. Mit dieser Hilfs-Exceltabelle kann man nun den Momentenverlauf solange anpassen, bis die gewünschte Höchstleistung erzielt wird.
Schritt B: Die Übersetzung
Der zweite große Komplex ist die Übersetzung, deren Parameter in der antrieb_constfile_D88.txt enthalten sind. Das Übersetzungsverhältnis wird mit "i" angegeben. Die Gesamtübersetzung setzt sich aus den Einzelübersetzungen zusammen:
i_ges = i_Gang * i_Achse.
Die Gangübersetzung ist das Drehzahlverhältnis zwischen Motor und Getriebe-Abtrieb (Kardanwelle zur Achse), die Achsübersetzung ist das Drehzahlverhältnis zwischen Kardanwelle und Rad. Folgt man der Kraft vom Motor zum Rad, wird die Drehzahl jeweils durch i geteilt und das Drehmoment mit i multipliziert:
Kardanwellendrehzahl = Motordrehzahl / i_Gang Kardanwellenmoment = Motormoment * i_Gang
Raddrehzahl = Kardanwellendrehzahl / i_Achse = Motordrehzahl / (i_Gang * i_Achse) Radmoment = Kardanwellenmoment * i_Achse = Motormoment * i_Gang * i_Achse
Die Konstanten für die Übersetzungsverhältnisse lauten:
- antrieb_getr_ratio1 (1,36 - der erste Gang beim Voith-Getriebe verhält sich aufgrund des Wandlereinsatzes anders als die höheren Gänge, weshalb hier dasselbe "formale" Übersetzungsverhältnis steht wie im 2. Gang)
- antrieb_getr_ratio2 (1,36)
- antrieb_getr_ratio3
- antrieb_i_achse
<UNFERTIG>